We’ll talk about the other networks and how they worked in a later post, for this post, let’s restrict our discussion to the architecture which researchers designed to answer the question that,
“Is learning better networks as easy as stacking more layers?”
The Problem
Vanishing Gradient Problem
The previous architectures which had been quiet successful relative to their competitors were made up by stacking multiple layers to form the final architecture, a problem that arises with this was when using activation functions like the sigmoid activation function, squishes a large input space into a small input space between 0 and 1, due to which even if there is a large change in the input of the sigmoid function, there will only be a small change in the output. This is better understood through the graph, which shows the behaviours of the sigmoid function and the derivative of the sigmoid function over a range.
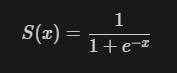
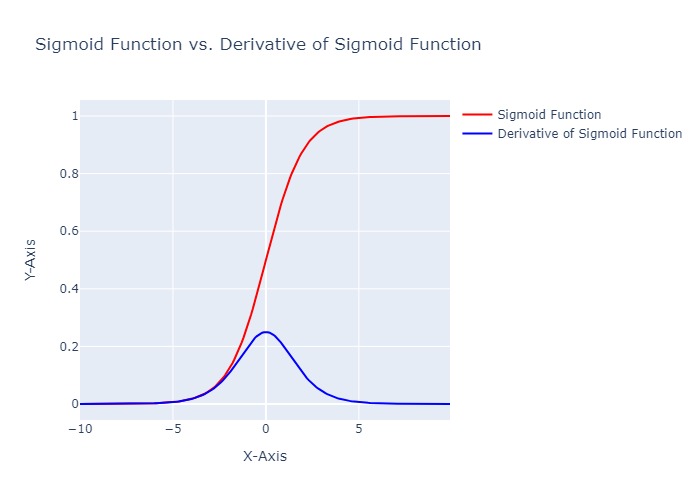
This problem is not so significant in shallow networks which use this activation, but as we keep on stacking more layers the problem starts to come up more significantly.
Gradients of neural networks are calculated using backpropagation, in backpropagation we find the derivative of the network by moving layer by layer from the final layer to the initial layer, and based on the chain rule of differentiation, the derivatives of each layer are multiplied down the network to compute the derivative for the initial layers.
When the hidden layers in these large networks use activation functions like sigmoid, a large number of these small derivative are multiplied together, which results in the gradient getting decreased exponentially as we move our way down to the initial layers of the network.
The initial layers which are crucial for identifying certain core elements and high level features in an input image, so it is important that the weights and biases of these layers are tuned in perfectly during the training process, but due to small gradients these layers are not effectively trained during the training process.
Accuracy Degradation
The authors also observed that, as the depth of the network was increasing, accuracy would get saturated after a point, this was expected to happen, let me tell you how,
When modelling the architecture we expect a sufficiently deep neural network to model all the intricacies of our data well, eventually this would lead to a stage when adding additional layers in the network would lead the network into completely learning the data. After this point if we go on to increase the depth of the network, the accuracy would not increase and also may start decreasing, this could simply be termed as an overfitting problem but this happens due to the additional layers in the architecture resulting in a higher training error.
Let us consider an architecture which has n layers, this architecture achieves an accuracy of x, now we consider another architecture with more layers than the previous architecture, let it have m layers clearly (m>n).
We could start by saying that this bigger network should at least be as good as the shallower network. How?
Consider replacing the first n layers of the deeper network with the trained n layers of the shallower network. Then, go on to replace the remaining m-n layers in the deeper network with an identity mapping. This should make the deeper network can easily learn the shallower models representation. Furthermore, we expect this deeper network to learn more complex representation of data if any is present.
But when practically applied, this is not what we say, in fact we say the accuracy decaying as we go on adding more and more layers.
This degradation is what led to the researchers in proposing a new repetitive block in the architecture called the Residual Block.
Residual Blocks
Instead of hoping each few stacked layers directly fit a desired underlying mapping, we explicitly let these layers fit a residual mapping.
The problem with traditional deep convolutional neural network based architectures was the fact that these architectures had a point after which adding more layers would saturate the accuracy and then eventually degrade which was not being caused by overfitting. This led to an intuition that, shallower networks are learning better than their deeper counterparts, although this sounds quite counter-intuitive, this is what was seen in practice.
A clear observation was that, shallower networks perform better than deeper networks with fewer more layers added to them, so why not go ahead and skip these extra layers and at least match the accuracy of the shallow sub-networks. This skipping of layers during training could be done using skip connections or residual connections.
Traditional neural networks were designed to work in a way in which the output of each layer is fed into the next layer. In case of a residual block, the layer feeds into the next layer and directly into the layers about 2-3 hops away from it.
This also helps the problem of vanishing gradient as during backpropagation, these skip connections could be really helpful in propagating larger gradients to the initial layers, and these layers could also learn as fast as the final layers, giving a better way to train deeper networks.
As a result of using these residual blocks and extensively working on the ImageNet classification dataset, in their CNN-based architecture, the authors show that:
- Extremely deep residual networks are easy to optimize, but the simple (stack-based) architectures exhibit a higher training error when the depth of architecture is increased.
- Deep Residual networks can easily enjoy accuracy gains from greatly increased depth, producing results substantially better than previous networks.
The model led to an ensemble have 3.57% top-5 error on the ImageNet classification test set, and won the 1st place in the ILSVRC 2015 classification competition.
The deeper representations of these residual networks have a excellent generalization performance on other recognition tasks, which led to the network winning 1st place on ImageNet Detection, ImageNet Localisation, COCO detection and COCO Segmentation in ILSVRC and COCO 2015 competition.
Further, I have gone ahead and implemented the DenseNet architecture with a detailed explaination of the code, in an interactive jupyter notebook, you can find it here.

123 Responses